Nombres triangulaires: Définition, Illustration et Propriétés

Nombres triangulaires: Définition, Illustration et Propriétés
(Source: fameuse page de Gupta, Shyam Sunder)

Définition des nombres triangulaires
Par définition, les nombres triangulaires sont formés par les sommes partielles des séries 1+2+3+4+5+6+7+...+(n-2)+(n-1)+n. Le n^eme nombre triangulaire peut s'écrire:
T_n = ½(n + 1)n ou encore T_n = ½(n² + n).
Ainsi :
T₁ = 1
T₂ = 1 + 2 = 3
T₃ = 1 + 2 + 3 = 6
T₄ = 1 + 2 + 3 + 4 = 10.
La séquence des nombres triangulaires est constituée par les nombres 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, ..., 595, 630, 666, 703, 741, ... Pour une plus longue liste, voir séquence A000217 de Sloane, N. J. A.

Les 100 premiers nombres triangulaires:

(En rouge, les nombres triangulaires pairs)

NOTES:
* 666 est le plus grand nombre triangulaire formé par des chiffres identiques.; 666 = T₃₆ = 1+2+3+4+5+6+7+...+35+36
* 666 est aussi un "nombre de Smith", i.e. la somme de ses chiffres [6+6+6] = 18 est égale à la somme de ses chiffres de ses facteurs premiers ou diviseurs [2+3+3+(3+7)] = 18.
* Il y a peu de chance que vous soyez né une "année triangulaire ", car lors du dernier siècle et ce, tel qu'il appert du tableau ci-dessus, la seule et unique année porte-bonheur était 1953 !!!

Preuve de la formule de calcul des nombres triangulaires

T_n = 1 + 2 + 3 + ...+ (n-2) + (n-1) + n    écriture de T_n dans l'ordre crossant;
T_n = n + (n-1) + (n-2) +... + 3 + 2 + 1    écriture de T_n dans l'ordre décrossant;
----------------------------------------
2T_n = n(n+1)          en additionnant 2 à 2 les deux relations ci-haut et en combinant les termes de droite par pair de (n+1); il y a n termes dans cette somme.
ou 2T_n = [1+n]+[2+(n-1)]+[3+(n-2)]+...+[(n-1)+2]+[n+1] = n(n+1)      donc:
T_n = n(n + 1)/2       ce qu'il fallait démontrer.

Anecdote sur Karl Friedrich Gauss: somme de 1 à 100

Relativement au fameux mathématicien Gauss (1777-1855), Walter Lietzmann rappote l'histoire suivante:
Dans son enfance, il avait à faire la somme cumulative des nombres 1 à 100. Son professeur était certain que cette opération occuperait Gauss pour un bon moment. Hélas! Karl Friedrich Gauss trouva la réponse 5050 après seulement quelques minutes. Au lieu d'additionner les nombres un après l'autre, Gauss fit des pairs de nombres de façon à pouvoir utiliser la multiplication:
1+2+3+4+...+50+51+...+97+98+99+100
= (1+100) + (2+99) + (3+98) + (4+97)+ ...+ (50+51)
= 50 x 101
= 5050

Illustrations des nombres triangulaires
Le nombre triangulaire est le nombre de "points" nécessaires pour construire un triangle, le tout tel qu'illustré ci-dessous:


   ☆     ☆      ☆          ☆           ☆
        ☆ ☆    ☆ ☆      ☆ ☆         ☆ ☆
                ☆ ☆ ☆   ☆ ☆ ☆      ☆ ☆ ☆
                         ☆ ☆ ☆ ☆    ☆ ☆ ☆ ☆
                                       ☆ ☆ ☆ ☆ ☆
   1   3      6       10         15

1 = T₁
3 = T₂ = 1 + 2
6 = T₃ = 1 + 2 + 3
10 = T₄ = 1 + 2 + 3 + 4
15 = T₅ = 1 + 2 + 3 + 4 + 5

(Source des deux images: Gupta, Shyam Sunder et Wolfram Mathworld)
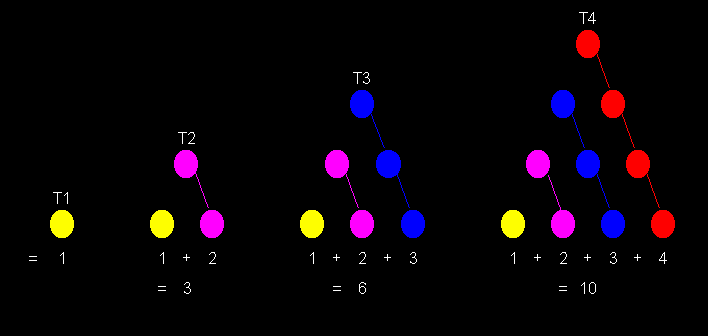
Nombres triangulaires et Triangle de Pascal
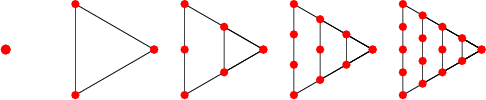
Les nombres triangulaires (en rouge) constituent les troisièmes diagonales du fameux triangle de Pascal:

								1									Rangée 0
							1		1								Rangée 1
						1		2		1							Rangée 2
					1		3		3		1						Rangée 3
				1		4		6		4		1					Rangée 4
			1		5		10		10		5		1				Rangée 5
		1		6		15		20		15		6		1			Rangée 6
	1		7		21		35		35		21		7		1		Rangée 7
1		8		28		56		70		56		28		8		1	Rangée 8

Triangle de Pascal à 19 rangées

1
1     1
1     2     1
1     3     3     1
1     4     6     4     1
1     5    10    10     5     1
1     6    15    20    15     6     1
1     7    21    35    35    21     7     1
1     8    28    56    70    56    28     8     1
1     9    36    84   126   126    84    36     9     1
1    10    45   120   210   252   210   120    45    10     1
1    11    55   165   330   462   462   330   165    55    11     1
1    12    66   220   495   792   924   792   495   220    66    12     1
1    13    78   286   715  1287  1716  1716  1287   715   286    78    13     1
1    14    91   364  1001  2002  3003  3432  3003  2002  1001   364    91    14     1
1    15   105   455  1365  3003  5005  6435  6435  5005  3003  1365   455   105    15     1
1    16   120   560  1820  4368  8008 11440 12870 11440  8008  4368  1820   560   120    16     1
1    17   136   680  2380  6188 12376 19448 24310 24310 19448 12376  6188  2380   680   136    17     1
1    18   153   816  3060  8568 18564 31824 43758 48620 43758 31824 18564  8568  3060   816   153    18     1
1    19   171   969  3876 11628 27132 50388 75582 92378 92378 75582 50388 27132 11628  3876   969   171    19     1

Propriétés des nombres triangulaires

Les multiples et curieuses propriétés des nombres triangulaires ont été étudiées par les anciens mathématiciens grecs, en particulier Pythagore. L'envolée d'oiseaux et le festival de vol artistique d'avions suivent le principe des nombres triangulaires.

PROPRIÉTÉ 1
Tous les nombres parfaits sont nombres triangulaires !!!

PROPRIÉTÉ 2
Tout nombre entier est la somme de trois (3! ... Trinité!) nombres triangulaires (démontré par Gauss). Plus généralement, Fermat énonçait en 1636 dans une conjecture que tout entier naturel peut s'écrire comme somme de n nombres polygonaux d'ordre n (3 nombres triangulaires, 4 nombres carrés, 5 nombres pentagonaux, etc.). Ce résultat fut prouvé par Lagrange pour n = 3, Legendre pour n = 4 et Cauchy prouva le cas général (1813).

PROPRIÉTÉ 3
Pour tout nombre naturel n, la somme 1 + 9 + 9² + 9³ + ... + 9ⁿ est un nombre triangulaire. Exemples:
1 = T₁
1 + 9 = T₄
1 + 9 + 9² = T₁₃
1 + 9 + 9² + 9³ = T₄₀
1 + 9 + 9² + 9³ + 9⁴ = T₁₂₁

PROPRIÉTÉ 4
La somme de deux nombres triangulaires consécutifs est toujours un nombre carré. Cette propriété découle simplement du théorème selon lequel la somme de deux nombres consécutifs est un carré.
T_n + T_n+1 = (n + 1)² ainsi:

T₁ + T₂ = 1 + 3 = 4 = 2²
T₂ + T₃ = 3 + 6 = 9 = 3²
T₃ + T₄ = 6 + 10 = 16 = 4²

PROPRIÉTÉ 5
La racine numérique d'un nombre triangulaire (i.e. la somme ultime de ses chiffres jusqu'à obtention d'un chiffre unique) est toujours 1, 3, 6 ou 9.

PROPRIÉTÉ 6
Un nombre triangulaire ne se termine jamais par les chiffres 2, 4, 7 ou 9.

PROPRIÉTÉ 7
Un nombre triangulaire plus grand que 1 ne peut jamais être une puissance cubique (de 3), ni puissance de 4 ou puissance de 5.

PROPRIÉTÉ 8
Si T est un nombre triangulaire alors 9T + 1 est aussi un nombre triangulaire (9+1 =10, le "plus parfait nombre" au sens de Pythagore). Exemples :
9T₁ + 1 = 9 x 1 + 1 = 10 = T₄
9T₂ + 1 = 9 x 3 + 1 = 28 = T₁₇

PROPRIÉTÉ 9
Si T est un nombre triangulaire alors 8T + 1 est toujours un carré parfait.
8T₁ + 1 = 8 x 1 + 1 = 9 = 3²
8T₂ + 1 = 8 x 3 + 1 = 25 = 5²

PROPRIÉTÉ 10
La somme de n cubes consécutifs débutant par l (l'Unité !) est égale au carré du n^eme nombre triangulaire i.e. (T_n)² = 1³ + 2³ + 3³ + ... + n³. Exemples:
(T₄)² = 10² = 100 = 1³ + 2³ + 3³ + 4³
(T₅)² = 15² = 225 = 1³ + 2³ + 3³ + 4³ + 5³

CURIEUSES IDENTITÉES

T₈ + T₃₅ + T₂₃ = T₉ + T₂₁ + T₃₆
avec 8 + 35 + 23 = 9 + 21 + 36

T₁ + T₂ + T₃ = T₄
T₅ + T₆ + T₇ + T₈ = T₉ + T₁₀
T₁₁ + T₁₂ + T₁₃ + T₁₄ + T₁₅ = T₁₆ + T₁₇ + T₁₈
T₁₉ + T₂₀ + T₂₁ + T₂₂ + T₂₃ + T₂₄ = T₂₅ + T₂₆ + T₂₇ + T₂₈
(T_n)²= T_n + T_n-1 x T_n+1
(T_n-1)² = 2T_n x T_n-1

Extensions du concept de nombre triangulaire
Le concept de nombre triangulaire se généralise à l'ensemble des formes géométriques associées à divers nombres "géométriques" dont les quadrilatères, les pentagones, les hexagones, etc.

Type - Géométrie	Formule	Série - Exemples
nombres triangulaires nombres carrés nombres pentagonaux nombres hexagonaux nombres heptagonaux nombres octogonaux ...	n(n+1)/2 n² n(3n-1)/2 n(4n-2)/2 n(5n-1)/2 n(6n-1)/2 ...	1 3 6 10 15 21 28... 1 4 9 16 25 36 49... 1 5 12 22 35 51 70... 1 6 15 28 45 66 91... 1 7 18 34 55 81 112... 1 8 21 40 65 96 133... ...

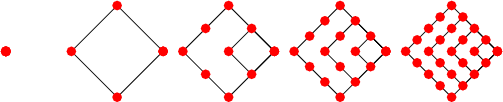(Notez en gras les nombres triangulaires retrouvés dans les formes géométriques plus larges)

Nombres carrés	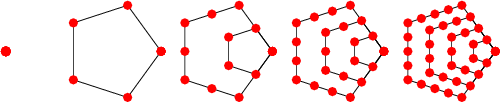Nombres pentagonaux
Nombres hexagonaux	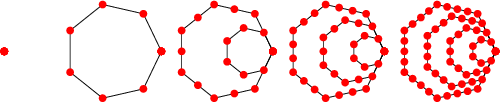Nombres heptagonaux
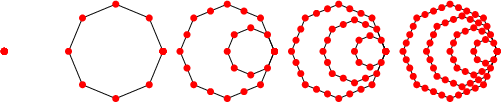Nombres octogonaux

(Source des images: MathWorld Wolfram)