666: Symbole de la Trinité divine

Site d'intérêt:

¤Partenaires¤:

Annuaire dbland
Annuaire id-aime
Annuaire Gratuit
Cadeaux

χξς	666	DCLXVI	וסם	ﻭﺱﺥ
Grec	Latin	Romain	Hébreu	Arabe

Webmaster: NOTE - Usagers I.E.: TOP menu pour meilleure navigation SANS pub; menu gauche pour description des liens
666: Symbole de la Trinité divine ...

Lien entre 666, son inverse graphique 999, 333 et 111
Chaque nombre du triplet (333, 666 et 999) s'écrit en fonction de 111 [l'Unité stable dans la Trinité divine ou trois personnes dans une] et donne toujours une racine numérique égale à 9.

TABLEAU T-1

333 = 111 x 3 = 111 + 111 + 111	⇒ 3 + 3 + 3 = 9
666 = 333 + 333 = 111 x 6 = 111 x 3 x 2	⇒ 6 + 6 + 6 = 18 ⇒ 1 + 8 = 9
999 = 666 + 333 = 111 x 9 = 111 x 3 x 3	⇒ 9 + 9 + 9 = 27 ⇒ 2 + 7 = 9

De plus, les puissances de chaque item du quatuor (111, 333, 666, 999) possèdent chaque fois la même racine numérique 9. Pour tout entier n les puissances à base de triplets 111ⁿ, 333ⁿ, 666ⁿ et 999ⁿ ont la même racine numérique.

TABLEAU T-2

111² = 12 321 ⇒ 9	111³ = 1 367 631 ⇒ 27 ⇒ 9	111⁴ = 151 807 041 ⇒ 27 ⇒ 9
333² = 110 889 ⇒ 27 ⇒ 9	333³ = 36 926 037 ⇒ 36 ⇒ 9	333⁴ = 12 296 370 321 ⇒ 36 ⇒ 9
666² = 443 556 ⇒ 27 ⇒ 9	666³ = 295 408 296 ⇒ 45 ⇒ 9	666⁴ = 196 741 925 136 ⇒ 54 ⇒ 9
999² = 998 001 ⇒ 27 ⇒ 9	999³ = 997 002 999 ⇒ 54 ⇒ 9	999⁴ = 996 005 996 001 ⇒ 54 ⇒ 9

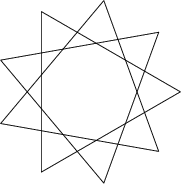Une bonne illustration graphique du lien entre les quatre triplets isomorphes (111, 333, 666 999) est l'Étoile de Goliath ou nonagramme, polygone 9/3 composé de 3 triangles équilatéraux [équipotence trinitaire ou égale puissance de chaque Unité de la Trinité divine] disposés en angles de 0°, 40° et 80°. Cette structure caractéristique du nonagramme engendre un polygone central à 9 côtés égaux, cerné par deux groupes de 9 figures identiques dont 9 autres triangles équilatéraux plus petits.

Écritures binaires des nombres 1, 3, 6 et 9
L'écriture binaire de chacun des nombres 1, 3, 6 et 9 est transcrite dans le tableau T-3. Voici le lien à suivre pour aller à notre moteur de Conversion binaire-décimale. Sous leurs formes binaires, les nombres 1 et 111, autres symboles de l'Unité dans la Trinité divine, ont des racines numériques respectives de 3 et 9 [3 x 3], des chiffres caractéristiques de l'Étoile de Goliath, un polygone 9/3. En écriture binaire, tous les items du triplet (333, 666, 999) conduisent à la même racine numérique finale 3 (la Trinité), avec chaque fois une racine numérique transitoire égale à 12 (la voie des 12 Apôtres). Notons que 12 = 3 x 4, ce dernier chiffre étant la racine numérique commune de 3, de 6 et de 9.

TABLEAU T-3

1 = 00110001 ⇒ 3	111 = 00110001 00110001 00110001 ⇒ 9
3 = 00110011 ⇒ 4	333 = 00110011 00110011 00110011 ⇒ 12 ⇒ 1 + 2 = 3
6 = 00110110 ⇒ 4	666 = 00110110 00110110 00110110 ⇒ 12 ⇒ 1 + 2 = 3
9 = 00111001 ⇒ 4	999 = 00111001 00111001 00111001 ⇒ 12 ⇒ 1 + 2 = 3

L'Unité dans la Trinité
L'Unité est symbolisée ici par le chiffre 37, dont la racine numérique est précisément égale à 1 [37 ⇒ 3 + 7 = 10 ⇒ 1 + 0 = 1]. L'Unité est contenue dans le triplet 666, ainsi que dans toutes les autres structures numériques trinitaires et isomorphes, à l'exception du triplet vide (000).

En outre, et tel qu'il appert de la première colonne du tableau T-4, toute structure trinitaire propre (i.e. non vide ou nulle) est à la fois le produit de sa composante spécifique [son Image, le chiffre à la base du triplet), de 3 [la Trinité] et de 37 [symbole ultime de l'Unité].

Les racines numériques transitoires des structures trinitaires correspondent exactement aux multiplicateurs respectifs de 37 et sont égales à 3, 6, 9, 12, 15, 18, 21 et 27, dans l'ordre. Les racines numériques finales prennent constamment mais de façon cyclique les seules valeurs 3 [= 1 x 3], 6 [= 2 x 3] et 9 [= 3 x 3], toutes divisibles par 1 [l'Unité] et par 3 [la Trinité].

TABLEAU T-4

111 = 1 x 3 x 37 = 3 x 37	⇒ 1 + 1 + 1 = 3
222 = 2 x 3 x 37 = 6 x 37	⇒ 2 + 2 + 2 = 6
333 = 3 x 3 x 37 = 9 x 37	⇒ 3 + 3 + 3 = 9
444 = 4 x 3 x 37 = 12 x 37	⇒ 4 + 4 + 4 = 12 ⇒ 1 + 2 = 3
555 = 5 x 3 x 37 = 15 x 37	⇒ 5 + 5 + 5 = 15 ⇒ 1 + 5 = 6
666 = 6 x 3 x 37 = 18 x 37	⇒ 6 + 6 + 6 = 18 ⇒ 1 + 8 = 9
777 = 7 x 3 x 37 = 21 x 37	⇒ 7 + 7 + 7 = 21 ⇒ 2 + 1 = 3
888 = 8 x 3 x 37 = 24 x 37	⇒ 8 + 8 + 8 = 24 ⇒ 2 + 4 = 6
999 = 9 x 3 x 37 = 27 x 37	⇒ 9 + 9 + 9 = 27 ⇒ 2 + 7 = 9

666 racine trinitaire de base
Considerons l'ensemble des neufs chiffres de base (à l'exclusion du zéro). Disposons les dans l'ordre en trois triplets et appliquons leur l'addition trinitaire en ligne puis en colonne. Les riches résultats de ces opérations fort simples sont contenus aux tableaux T-5a et T-5b. Les racines numériques des trois sommes en ligne donnent le triple six (666). Toutefois, les totaux en colonne engendrent le triplet particulier de racines numériques (3, 6, 9), nombres cycliques du tableau T-4. Par ailleurs, le grand total des lignes est exactement égal au grand total des colonnes, soit 45, avec une racine numérique de 9, identique à celle de la somme du dernier triplet [3 + 6 + 9 = 18 ⇒ 1 + 8 = 9].

TABLEAU T-5a Somme en ligne

1 + 2 + 3 = 6	⇒ 6
4 + 5 + 6 = 15	⇒ 1 + 5 = 6
7 + 8 + 9 = 24	⇒ 2 + 4 = 6
6 + 15 + 24 = 45	⇒ 4 + 5 = 9

TABLEAU T-5b Somme en colonne

1 + 4 + 7 = 12	⇒ 1 + 2 = 3
2 + 5 + 8 = 15	⇒ 1 + 5 = 6
3 + 6 + 9 = 18	⇒ 1 + 8 = 9
12 + 15 + 18 = 45	⇒ 4 + 5 = 9

Nombre 9: inverse graphique du 6 et racine du triple cycle trinitaire (3, 6, 9)
Le nombre 9 est la racine numérique de la somme de l'ensemble des structures numériques trinitaires et isomorphes (total de 4 995). Tel qu'il appert de le seconde ligne du tableau T-6, le nombre 9 est également la racine numérique du triple cycle trinitaire (3, 6, 9), un résultat conforme à la structure exposée au tableau T-4.

TABLEAU T-6

111+222+333+444+555+666+777+888+999 = 4 995	⇒ 4 + 9 + 9 + 5 = 27 ⇒ 2 + 7 = 9
(3 x 3) + (6 x 3) + (9 x 3) = 9 + 18 + 27 = 54	⇒ 5 + 4 = 9

666: Mythe bivalent