Webmaster: NOTICE - I.E. Users: TOP menu for best navigation and NO ads; left menu for links description
666: Symbol of the Divine Trinity ...
Link between 666, its graphic reverse 999, 333 and 111
Each number of the triplet (333, 666 and 999) is written according to 111 [the stable Unit in the divine Trinity or three persons in one] and always gives a numerical root equalizes to 9.
TABLE T-1
| 333 = 111 x 3 = 111 + 111 + 111 |
⇒ 3 + 3 + 3 = 9 |
| 666 = 333 + 333 = 111 x 6 = 111 x 3 x 2 |
⇒ 6 + 6 + 6 = 18 ⇒ 1 + 8 = 9 |
| 999 = 666 + 333 = 111 x 9 = 111 x 3 x 3 |
⇒ 9 + 9 + 9 = 27 ⇒ 2 + 7 = 9 |
Moreover, the powers of each item of the quartet (111, 333, 666, 999) have each time the same numerical root 9. For any whole number n the powers containing triplets 111n, 333n, 666n and 999n have the same numerical root.
TABLE T-2
| 1112 = 12 321 ⇒ 9 |
1113 = 1 367 631 ⇒ 27 ⇒ 9 |
1114 = 151 807 041 ⇒ 27 ⇒ 9 |
| 3332 = 110 889 ⇒ 27 ⇒ 9 |
3333 = 36 926 037 ⇒ 36 ⇒ 9 |
3334 = 12 296 370 321 ⇒ 36 ⇒ 9 |
| 6662 = 443 556 ⇒ 27 ⇒ 9 |
6663 = 295 408 296 ⇒ 45 ⇒ 9 |
6664 = 196 741 925 136 ⇒ 54 ⇒ 9 |
| 9992 = 998 001 ⇒ 27 ⇒ 9 |
9993 = 997 002 999 ⇒ 54 ⇒ 9 |
9994 = 996 005 996 001 ⇒ 54 ⇒ 9 |
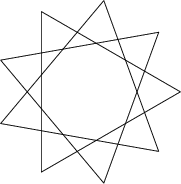 |
A good graphic illustration of the link between the four isomorphous triplets (111, 333, 666 999) is the Star of Goliath or nonagramm, polygon 9/3 composed of 3 equilateral triangles [trinitary equipotence or equal power of each Unit of the divine Trinity] laid out in angles of 0°, 40° and 80°.
This characteristic structure of the nonagramm generates a central polygon with 9 equal sides, encircled by two groups of 9 identical figures including 9 other smaller equilateral triangles.
|
Binary writings of numbers 1, 3, 6 and 9
The binary writing of each of the numbers 1, 3, 6 and 9 is transcribed in Table T-3. Here is the link to follow to go to our engine of Binary to decimal conversion.
In their binary formats, numbers 1 and 111, other symbols of the Unit in the divine Trinity, have respective numerical roots of 3 and 9 [3 x 3], characteristic figures of the Star of Goliath, a polygon 9/3.
In binary writing, all the items of the triplet (333, 666, 999) lead to the same final numerical root 3 (the Trinity), with each time a transitory numerical root equal to 12 (the way of the 12 Apostles). Let us note that 12 = 3 X 4, this last figure being the common numerical root of 3, 6 and 9.
TABLE T-3
| 1 = 00110001 ⇒ 3 |
111 = 00110001 00110001 00110001 ⇒ 9 |
| 3 = 00110011 ⇒ 4 |
333 = 00110011 00110011 00110011 ⇒ 12 ⇒ 1 + 2 = 3 |
| 6 = 00110110 ⇒ 4 |
666 = 00110110 00110110 00110110 ⇒ 12 ⇒ 1 + 2 = 3 |
| 9 = 00111001 ⇒ 4 |
999 = 00111001 00111001 00111001 ⇒ 12 ⇒ 1 + 2 = 3 |
Unity in Trinity
The Unit is symbolized here by the figure 37, of which the numerical root is precisely equal to 1 [37 ⇒ 3 + 7 = 10 ⇒ 1 + 0 = 1]. The Unit is contained in triplet 666, like in all the other numerical trinitary and isomorphous structures, except for the empty triplet (000).
Moreover, and such as it comes to ligth from the first column of table T-4, any true trinitary structure (i.e. not vacuum or null) is at the same time the product of his specific component [his Image, the figure at the base of the triplet), of 3 [the Trinity] and of 37 [ultimate symbol of the Unit].
The transitory numerical roots of the trinitary structures correspond exactly to the respective multipliers of 37 and are equal to 3, 6, 9, 12, 15, 18, 21 and 27, in the order. The final numerical roots take constantly but in a cyclic way only values
3 [= 1 x 3], 6 [= 2 x 3] et 9 [= 3 x 3], all divisible by 1 [the Unit] and 3 [the Trinity].
TABLE T-4
| 111 = 1 x 3 x 37 = 3 x 37 |
⇒ 1 + 1 + 1 = 3 |
| 222 = 2 x 3 x 37 = 6 x 37 |
⇒ 2 + 2 + 2 = 6 |
| 333 = 3 x 3 x 37 = 9 x 37 |
⇒ 3 + 3 + 3 = 9 |
| 444 = 4 x 3 x 37 = 12 x 37 |
⇒ 4 + 4 + 4 = 12 ⇒ 1 + 2 = 3 |
| 555 = 5 x 3 x 37 = 15 x 37 |
⇒ 5 + 5 + 5 = 15 ⇒ 1 + 5 = 6 |
| 666 = 6 x 3 x 37 = 18 x 37 |
⇒ 6 + 6 + 6 = 18 ⇒ 1 + 8 = 9 |
| 777 = 7 x 3 x 37 = 21 x 37 |
⇒ 7 + 7 + 7 = 21 ⇒ 2 + 1 = 3 |
| 888 = 8 x 3 x 37 = 24 x 37 |
⇒ 8 + 8 + 8 = 24 ⇒ 2 + 4 = 6 |
| 999 = 9 x 3 x 37 = 27 x 37 |
⇒ 9 + 9 + 9 = 27 ⇒ 2 + 7 = 9 |
666 basic trinitary root
Consider the whole of the nine basic figures (other than the zero). Let us lay out them in the order in three triplets and apply to them the trinitary addition in line then in column. The rich results of these extremely simple operations are contained in tables T-5a and T-5b.
The numerical roots of the three sums on line give triple six (666). However, the totals in column generate the particular triplet of numerical roots (3, 6, 9), cyclic numbers of table T-4.
In addition, the great total of the lines is exactly equal to the great total of the columns, that is to say 45, with a root numerical of 9, identical to that of the sum of the last triplet [3 + 6 + 9 = 18 ⇒ 1 + 8 = 9].
TABLE T-5a Sum by line
| 1 + 2 + 3 = 6 |
⇒ 6 |
| 4 + 5 + 6 = 15 |
⇒ 1 + 5 = 6 |
| 7 + 8 + 9 = 24 |
⇒ 2 + 4 = 6 |
| 6 + 15 + 24 = 45 |
⇒ 4 + 5 = 9 |
|
TABLE T-5b Sum by column
| 1 + 4 + 7 = 12 |
⇒ 1 + 2 = 3 |
| 2 + 5 + 8 = 15 |
⇒ 1 + 5 = 6 |
| 3 + 6 + 9 = 18 |
⇒ 1 + 8 = 9 |
| 12 + 15 + 18 = 45 |
⇒ 4 + 5 = 9 |
|
Numbers 9: opposite graph of the 6 and root of triple trinitary cycle (3, 6, 9)
Number 9 is the numerical root of the sum of the whole of the trinitary and isomorphous numerical structures (total of 4 995). Such as it comes to light from the second line of table T-6, number 9 is also the numerical root of triple trinitary cycle (3, 6, 9), a result in conformity with the exposed structure in table T-4.
TABLE T-6
| 111+222+333+444+555+666+777+888+999 = 4 995 |
⇒ 4 + 9 + 9 + 5 = 27 ⇒ 2 + 7 = 9 |
| (3 x 3) + (6 x 3) + (9 x 3) = 9 + 18 + 27 = 54 |
⇒ 5 + 4 = 9 |
I-Recommend Internet DirectoryStatic directory listings for our reciprocal partners
All rights reserved666: Bivalent Myth
 |
|

