
Le calendrier perpétuel Moret propose une méthode permettant de calculer le jour de la semaine à partir d'une date donnée (Ex: 13 octobre 1307, un vendredi). Il consiste en une suite de trois tableaux dans lesquels on choisit successivement le siècle, l'année, le mois et le quantième (jour du mois). Vous pouvez télécharger (196 ko) ici une version imprimable au format PDF de ce calendrier Moret.
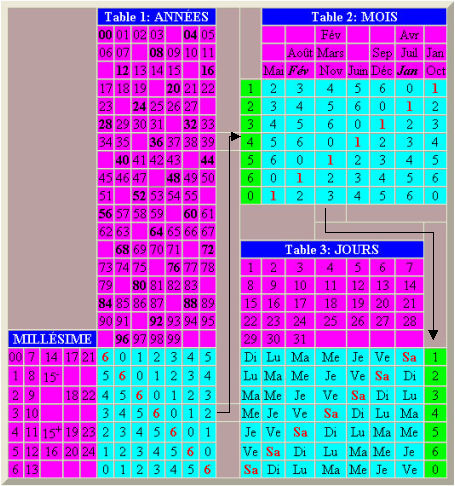
Calcul du jour de la semaine
Le calcul du jour de la semaine, à partir d'une date donnée, s'effectue en 3 étapes associées aux 3 tables ci-dessus.
1) Identifier l'année dans la table 1, en croisant son millésisme (2 premiers chiffres de l'année) et l'année proprement dite (2 derniers chiffres de l'année). Ce croisement permet d'obtenir un nombre, compris entre 0 et 6, dans le carré à fond bleu-clair de la table 1.
2) Reporter ce nombre à la colonne verdâtre dans la table 2 et le croiser avec le mois. Ce nouveau croisement donne un deuxième nombre, compris entre 0 et 6, dans le carré à fond bleu-clair de la table 2.
3) Reporter ce dernier nombre à la colonne verdâtre dans la table 3 et croiser le avec la date du mois (entre 1 et 31) pour enfin obtenir le jour de semaine.
Notes :
En gras, les années bissextiles (i.e. divisibles par 4); soulignons toutefois que les années séculaires (comme 1700, 1800 ou 1900) ne sont pas bissextiles, sauf celles dont les deux premiers chiffres sont divisibles par 4, comme 1600, 2000, 2400, 2800, etc. (pour détails, voir ce lien sur la Recherche des années bissextiles).
15- : Calendrier julien, dates jusqu'au 4 octobre 1582.
15+ : Calendrier grégorien, dates depuis le 15 octobre 1582.
Jan; Fév (en italique) : Colonne à utiliser si l'année est bissextile.
Il importe de noter les belles symétries par rapport aux diagonales des 3 carrés 7x7 de fond bleu-clair. Cela est lié au fait de la réccurence dans l'ordre des 7 jours de semaines, ces derniers pouvant être codés de 0 à 6; Ve = 0, Sa = 1, Di = 2, Lu = 3, Ma = 4, Me = 5 et Je = 6.
Exemples de calcul du jour de la semaine
| DATE | Lecture et Croisements dans les Tables | ||
| Table 1 | Table 2 | Table 3 | |
| 13 oct 1307* | 1 | 1 | Vendredi |
| 15 oct 1582 | 6 | 6 | Vendredi |
| 13 fév / mars 1609 | 5 | 1 | Vendredi |
| 13 fév / mars 1711 | 5 | 1 | Vendredi |
| 13 fév / mars 1857 | 5 | 1 | Vendredi |
| 13 fév / mars 1903 | 5 | 1 | Vendredi |
| 13 fév / mars 1953 | 5 | 1 | Vendredi |
| 13 fév 1976 (année bissextile) | 6 | 1 (et non 2) | Vendredi |
| 13 jan 1984 (année bissextile) | 2 | 1 (et non 2) | Vendredi |
| 13 fév / mars 1998 | 5 | 1 | Vendredi |
| 13 mai 2005 | 0 | 1 | Vendredi |
| 13 jan 2006 | 1 | 1 | Vendredi |
| 13 fév / mars 2009 | 5 | 1 | Vendredi |
D'où la malédiction du vendredi 13 selon ses disciples contemporains!
NOTE: Une année donnée comportera 2 (deux) vendredis 13 consécutifs mensuellement [fait extrêmement rare] si et seulement si il s'agit une année normale dont le 1er jour est un jeudi (exemple = 1998, en févier et mars). Ce phénomène rare se produit uniquement aux mois de févier et mars. Lors du denier siècle, cela est survenu seulement 11 fois en 100 ans, soit en 1903, 1914, 1925, 1931, 1942, 1953, 1959, 1970, 1981, 1987 et 1998.
Vérification des résultats de calcul du jour de la semaine
Au besoin, le lecteur pouurait vérifier ses résultats de calcul du jour de la semaine au moyen de notre Calendrier pratique, du Calendrier permanent ou du Calendrier perpétuel à 12 mois.
Remarques sur la logique de codification des jours de semaine
La semaine comporte sept jours, des jours se suivent dans un ordre préétabli, sans qu'il soit nécessaire de se fixer une origine.
On peut alors effectuer ce que les mathématiciens appellent une bijection de l'ensemble des sept jours de la semaine sur l'ensemble des sept premières lettres de l'alphabet de telle sorte à obtenir la suite répétive, terme pour terme, ci-après :
... A, B, C, D, E, F, G, A, B, C, D, E, F, G, A, B, C, D, E, F, G, A, B, C, D, E, F, G...
Il y a en tout et pour tout sept façons possibles de le faire :
Si Dimanche est A, Lundi sera B, Mardi sera C, Mercredi sera D, Jeudi sera E, Vendredi sera F et Samedi G.
Si Dimanche est B, Lundi sera C, Mardi sera D, Mercredi sera E, Jeudi sera F, Vendredi sera G et Samedi A.
Si Dimanche est C, Lundi sera D, Mardi sera E, Mercredi sera F, Jeudi sera G, Vendredi sera A et Samedi B.
Si Dimanche est D, Lundi sera E, Mardi sera F, Mercredi sera G, Jeudi sera A, Vendredi sera B et Samedi C.
Si Dimanche est E, Lundi sera F, Mardi sera G, Mercredi sera A, Jeudi sera B, Vendredi sera C et Samedi D.
Si Dimanche est F, Lundi sera G, Mardi sera A, Mercredi sera B, Jeudi sera C, Vendredi sera D et Samedi E.
Si Dimanche est G, Lundi sera A, Mardi sera B, Mercredi sera C, Jeudi sera D, Vendredi sera E et Samedi F.
Il suffit donc de connaître la lettre associée à Dimanche pour maîtriser cette bijection ; cette lettre s'appelle la lettre dominicale.
Si nous utilisons les diverses valeurs spécifiques de Mod(7), soit les nombres 0 à 6, nous obtenons un carré 7x7 ci-dessous, associé aux 7 bijections possibles de l'ensemble des sept jours de la semaine :
| Di | Lu | Ma | Me | Je | Ve | Sa |
| 6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 5 | 6 | 0 | 1 | 2 | 3 | 4 |
| 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 0 | 1 | 2 |
| 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Notons que ce dernier tableau est à la fois identique au carré à fond bleu-clair de la table 1 et isomorphe (même forme) aux deux autres carrés à fond bleu-clair des tables 2 et 3. Ce qui explique la correspondance implicite entre les trois tables.
Au besoin, le lecteur pourrait vérifier ses résultats de calcul du jour de la semaine au moyen de notre Calendrier pratique, du Calendrier permanent ou du Calendrier perpétuel à 12 mois.
Mythe du vendredi 13 |